Combining Kd's: demo using kinetic modeling in scipy

Predicting tautomer and protonation states seemed to me like a soluble problem, until I tried it (see Roger Sayle's So You Think You Understand Tautomerism). Even if you could accurately predict the population of a tautomer or protonated state of a ligand, what affect does that have on binding affinity to a protein? There is an equation for that, and this post simulates it with some kinetic models.

A reasonably common use case for the equation is where a (de)protonated atom engages in a hydrogen bond within a protein binding site. Changing the protonation state of the atom would lead to a repulsive HBD-HBD or HBA-HBA interaction, which presumably kills affinity. Sometimes, this is described by saying that the pKa of that atom is shifted in the binding site, so you observe more of the most potent species, but I prefer to think of it the other way round - the pKa of that atom is well-defined only in bulk solvent, but only ligands of the correct protonation state will bind. This is akin to conformational selection vs induced fit. The 'conformational selection' interpretation says that the ratio of protonated to unprotonated ligand in the site (if you could measure it) is shifted because the most potent species binds more often, after choosing its protonation/tautomer state. There are situations in enzymes where protonation of a ligand is caused by binding near a single water molecule with the correct geometry, but today's code demo doesn't consider that.

The demo in the notebook linked above, and inline below, uses kinetic modeling of reversible reactions to verify (in my head) an equation in the literature that is proposed for combining the Kd of two ligand protomers. This 'master equation' relates the Kd's of multiple tautomer/protonation states into a unified Kd value, which is necessarily what you would observe in experiment since you can't isolate a ligand species to measure it's Kd individually. A reversible reaction, in this case, refers to the reversible change in hydrogen count across atoms in a ligand (changing tautomers), or between a ligand and bulk water (changing protonation state), or indeed the formation of a ligand-receptor complex from the unbound states (the typical R+L <-> RL reaction).

The equation is here - note the 'k' is an association constant, so 1/Kd:

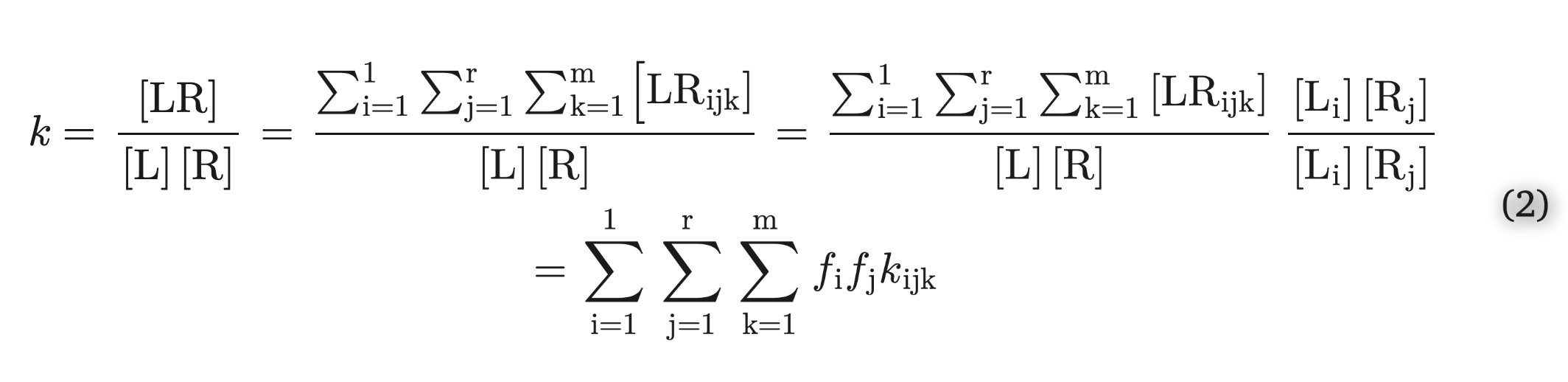
This equation matches up quite nicely with the simulation, without any optimization to make it fit. "Matching up" means that the combined Kd, according to the equation, is close to the Kd generated by the simulation.

The up-shot is this: when combining Kd's, the quantity that shifts your experimentally-observed Kd is the population of the potent ligand in the free, un-bound state, and not the change in pKa in the bound-state. So if you have a tautomer with fantastic potency, but has less than 1% population in solution, your observed Kd won't be fantastic anymore.

Keep in mind that it works for protein conformations, too: if you predict some ensemble conformations of a protein, and happen to choose a conformation with a rare cryptic site for your virtual screen, then potencies will suffer. Note that Kd is a thermodynamic quantity, not kinetic, so I'm sure there's some additional subtlety around reaction rates that would adjust this - see also Dan Erlanson's comments about cryptic sites exposed by fast-moving rotamer states vs slow-moving main-chain movement.

Finally: if the simulation is boring, see the final few cells of the notebook for a rule-of-thumb on how to penalise the Kd of a rare tautomer. That's if you know how to predict tautomer populations, anyway!