Spline regression demo

The snippet from two posts ago demonstrated how to calculate solvation energy, according to the HCT model, using numpy. We'll move now to the GBNeck model - but first, some notes on terminology. The HCT model was so named because it was published by Hawkins, Cramer, and Truhlar. It assumed that each atom occludes one VDW sphere of solvent. Subsequently experience showed this approximation is OK for small molecules but, for larger molecules (proteins) where you have atoms that are completely buried, the approximation diverges from reality. The problem is in the calculation of the Born radius, which is underestimated thanks to assuming that the interstices between atoms are filled with solvent, even if they couldn't fit a whole, discrete, water molecule. And so Onufriev, Bashford, and Case published an update to rescale the Born radii, which is now referred to as OBC. I always go to the OpenMM docs to find a table of AMBER names (e.g. igb1, igb2...), jargon names, and references for these solvation models.

Nevertheless, the OBC rescaling doesn't entirely fix the problem of counting up occupied volume. When two atoms are close together, there is a collar of volume that is excluded from solvent. Mongan et al refer to this as a 'neck' (shaded region):

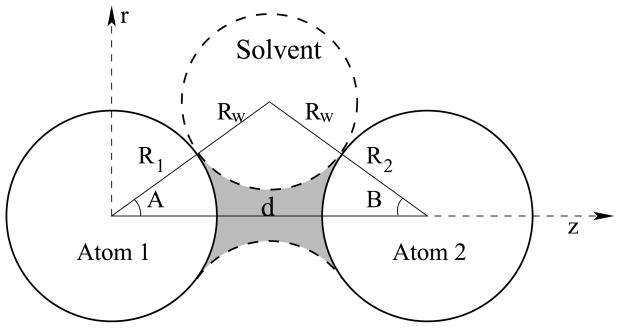
When there are multiple atoms nearby, the occluded shape would be more complex, but this additive, pairwise approximation seems to improve the performance. It's slow to calculate how this volume contributes to solvation on the fly, but the GBNeck paper describes an approximation of the approximation that is much faster, making it amenable for MD.

This snippet demonstrates how to calculate GBNeck2 solvation energy using numpy, which is relatively straightforward to plug in to scoring functions or to make differentiable.